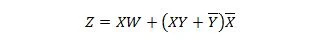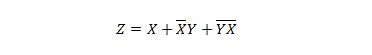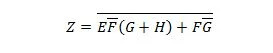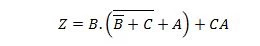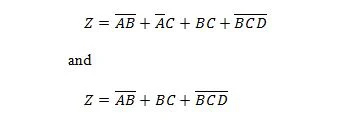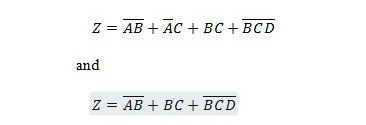Rozdział 2: Algebra Boole'a i powiązane z nią komponenty komputerowe
2.1 Podstawowe operatory logiczne
Załóżmy, że ja (autor) jestem wysoki i ty (czytelnik) jesteś wysoki. Gdyby ktoś zapytał Cię, czy oboje jesteśmy wysocy, odpowiedziałbyś „Tak” (prawda). Jeśli zapyta, czy oboje jesteśmy niscy, odpowiesz „Nie” (fałsz). Jeśli jesteś niski, a ja wysoki, a on zapyta cię, czy ty, czy ja jesteśmy wysocy, twoja odpowiedź będzie brzmiała „Tak” (prawda). Gdyby zapytał, czy oboje jesteśmy wysocy, nie otrzymałabyś odpowiedzi. Można dalej powiedzieć, że nie należy zadawać ostatniego pytania lub że na to pytanie nie ma odpowiedzi. Otóż chcę, abyś (czytelnik) wiedział, że dzisiaj w pewnych okolicznościach takie pytanie powinno zostać zadane.
W biologii człowiek jest albo wysoki, albo niski. To warunki „środowiskowe” sprawiają, że dana osoba ma średni wzrost. Jeden z naukowców, George Boole, zdefiniował zestaw odpowiedzi lub reguł dotyczących tego rodzaju pytań. Zasady te poznamy w tej części kursu kariery online (rozdział). Zasady te są dziś stosowane w informatyce, programowaniu, elektronice i telekomunikacji. Tak naprawdę bez tych zasad nie miałbyś komputera, jak to jest obecnie powszechne; nie mielibyście też programowania, jak to jest dzisiaj powszechne.
Prawda czy fałsz
Proste stwierdzenie w języku ludzkim jest samo w sobie albo prawdziwe, albo fałszywe. Jeśli powiem: „Jestem wysoki”, będzie to albo prawda, albo fałsz. Jeśli powiem „jesteś wysoki”, będzie to albo prawda, albo fałsz. Jeśli ja jestem wysoki, a ty niski i zadawane jest pytanie, czy oboje jesteśmy wysocy, w logice logicznej należy podać odpowiedź prawda lub fałsz. Który z tych dwóch należy podać? Boole tak naprawdę nie odpowiedział na to pytanie. Po prostu ustalił dla nas zbiór zasad, których powinniśmy przestrzegać. Dobra wiadomość jest taka, że jeśli zastosujesz się do tych zasad we właściwym kontekście, nie będziesz mieć żadnych dwuznaczności. Dzięki tym zasadom mamy dziś komputery i programowanie. Zasady są ci teraz dane. Zasad nie da się tak naprawdę wyjaśnić; po prostu je akceptujesz. Reguły są podzielone na trzy nagłówki: AND, OR i NOT.
I
Pytanie można zadać, jeśli zarówno Ty, jak i ja jesteśmy wysocy. Mój wzrost i Twój wzrost są następnie łączone za pomocą zestawu reguł ORAZ. Oto zasady ORAZ, których należy przestrzegać:
fałsz ORAZ fałsz = fałsz
fałsz ORAZ prawda = fałsz
prawda ORAZ fałsz = fałsz
prawda ORAZ prawda = prawda
Niech teraz wysoki będzie prawdziwy, a niski fałszywy. Oznacza to, że jeśli ja jestem niski ORAZ ty jesteś niski, ty i ja jesteśmy niscy. Jeśli jestem niski ORAZ ty jesteś wysoki, ty i ja jesteśmy niscy; to jest odpowiedź logiczna, którą musisz zaakceptować. Jeśli ja jestem wysoki ORAZ ty jesteś niski, zarówno ty, jak i ja jesteśmy niscy. Jeśli jestem wysoki ORAZ ty jesteś wysoki, ty i ja jesteśmy wysocy. Wszystko to są reguły logiczne ORAZ, które ty (czytelnik) musisz po prostu zaakceptować.
LUB
Pytanie można zadać, jeśli ty LUB ja jesteśmy wysocy. Mój wzrost i Twój wzrost są następnie łączone za pomocą zestawu reguł OR. Oto zasady LUB, których należy przestrzegać:
fałsz LUB fałsz = fałsz
fałsz LUB prawda = prawda
prawda LUB fałsz = prawda
prawda LUB prawda = prawda
Powtórzę raz jeszcze: niech wysoki będzie prawdziwy, a niski fałszywy. Oznacza to, że jeśli ja jestem niski LUB ty jesteś niski, ty LUB ja jestem niski. Jeśli jestem niski LUB ty jesteś wysoki, ty lub ja jesteśmy wysocy. Jeśli jestem wysoki LUB ty jesteś niski, ty LUB ja jestem wysoki. Jeśli jestem wysoki LUB ty jesteś wysoki, ty lub ja jesteśmy wysocy. Wszystko to są reguły logiczne, które musisz zaakceptować.
NIE
Teraz, w logice Boole'a, istnieją tylko dwa stany (możliwe odpowiedzi). Oznacza to, że jeśli NIE jesteś wysoki, jesteś niski. Jeśli NIE jesteś niski, jesteś wysoki; nic więcej. Oto zasady, których NIE należy przestrzegać:
NIE fałsz = prawda
NIE prawda = fałsz
Załóżmy, że masz sznurek (lub sprężynę), który możesz rozciągnąć (pociągnąć). Kiedy struna jest w swoim naturalnym stanie, jeśli powiem „NIE krótka”, przedłużysz ją; taka jest interpretacja. Gdy struna jest rozciągnięta, jeśli powiem „NIE długo”, pozwolisz, aby się skurczyła; taka jest interpretacja.
Musisz zapamiętać wszystkie podane zasady w różnych kategoriach.
Więcej niż dwa operandy
W języku komputerowym operatory AND, OR i NOT nazywane są operatorami. W przypadku operatora NOT potrzebny jest tylko jeden operand (wartość operatora), aby uzyskać odpowiedź. W przypadku operatorów AND i OR można mieć więcej niż dwa operandy. W poprzednich przypadkach pokazano dwa operandy dla AND i OR. Możesz mieć trzy operandy dla AND w następujący sposób:
fałsz ORAZ fałsz ORAZ fałsz = fałsz
fałsz ORAZ fałsz ORAZ prawda = fałsz
To są dwie linie; każdy ma dwa operatory AND. W rzeczywistości jest dziewięć wierszy, gdy operandów jest trzy. W przypadku operatora AND tylko ostatnia linia (dziewiąta linia) ma wartość true; wszystkie poprzednie wiersze są fałszywe. Zauważ, że w przypadku dwóch operandów AND tylko ostatnia linia jest nadal prawdziwa; wszystkie poprzednie trzy linie są fałszywe. Gdy operandów jest cztery, jest 16 linii i tylko ostatnia linia jest prawdziwa dla operatora AND.
Wzór AND i wzór OR są różne. Z trzema operandami dla dwóch operatorów OR, istnieje również dziewięć linii i tylko pierwsza linia, tym razem, jest fałszywa. Wiersz od drugiego do dziewiątego jest prawdziwy. Zauważ, że w przypadku dwóch operandów OR tylko pierwsza linia jest nadal prawdziwa; wszystkie pozostałe trzy linie są fałszywe. Gdy operandy dla OR wynoszą cztery, istnieje również 16 linii.
Operator NOT zajmuje się tylko jednym operandem. NIE fałsz jest prawdą, a NIE prawda jest fałszem.
2.2 Tabela prawdy z dwoma argumentami i ich komponenty elektroniczne
W matematyce istnieje temat zwany algebrą. Niewielką jego część widzieliśmy w poprzednim rozdziale. Istnieje rodzaj algebry zwany algebrą Boole’a. W algebrze Boole'a prawda jest identyfikowana przez dwucyfrową podstawę, która wynosi 1, a fałsz jest identyfikowany przez dwucyfrową podstawę, która wynosi 0.
Wewnętrzne elementy jednostki komputerowej są elementami elektronicznymi. Jednostka systemowa systemu komputerowego zawiera cyfrowe komponenty elektroniczne. Operację AND wykonuje mały element elektroniczny zwany bramką AND. Operację OR wykonuje mały element elektroniczny zwany bramką OR. Operację NOT wykonuje mały element elektroniczny zwany bramką NOT. Zbyt wiele z tych bramek może znajdować się w układzie scalonym (IC).
ORAZ Stół Prawdy i jego Brama
Poniższa tabela przedstawia tabelę prawdy AND i jej symbol bramki AND (mały obwód):
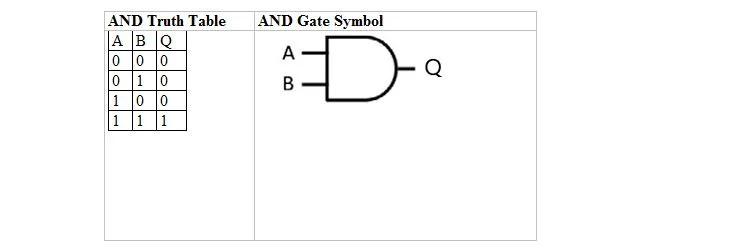
Zarówno w przypadku tabeli prawdy AND, jak i jej bramki, A i B są dwiema zmiennymi wejściowymi. Q jest zmienną wyjściową. A wynosi 1 lub 0. B wynosi 1 lub 0. Q wynosi 1 lub 0. Tabela prawdy AND z jedynkami i zerami jest taka sama jak poprzedni układ prawda/fałsz ORAZ (tabela). Równanie ORAZ to:
A . B = P
gdzie kropka (.) oznacza AND (boolean). Kropkę można pominąć, aby mieć AB = Q, co oznacza to samo (AND).
Uwaga: Bity A i B w czterech rzędach, jako pary, to pierwsze cztery liczby o podstawie drugiej rozpoczynające się od 0 (lub 00), tj. 00, 01, 10, 11.
Poniższa tabela przedstawia tabelę prawdy OR i jej symbol bramki OR (mały obwód):
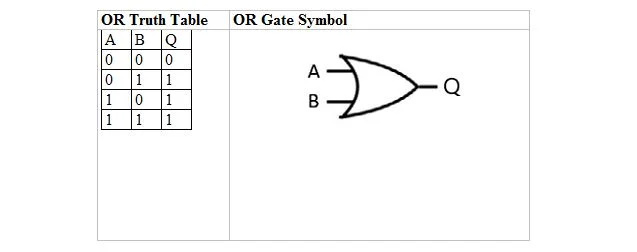
Zarówno w przypadku tabeli prawdy OR, jak i jej bramki, A i B są dwiema zmiennymi wejściowymi. Q jest zmienną wyjściową. Tabela prawdy LUB z jedynekami i zerami jest taka sama jak poprzedni układ prawdy LUB (tabela).
Równanie OR to:
A + B = Q
Gdzie + oznacza tutaj wartość logiczną OR, a nie dodawanie. Równanie odczytuje się jako „A lub B równe Q”.
Poniższa tabela przedstawia tabelę prawdy NOT i jej symbol bramki NOT (mały obwód):
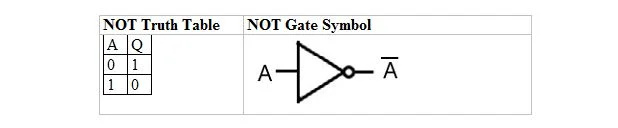
Tabela prawdy NOT lub bramka NOT ma tylko jedno wejście i jedno wyjście. Gdy na wejściu jest 0, na wyjściu jest 1. Gdy na wejściu jest 1, na wyjściu jest 0. Bramka NOT wykonuje rodzaj inwersji. Zmienna wyjściowa jest taka sama jak zmienna wejściowa, ale zawiera słupek (przekreślony). Tabela prawdy NOT zawierająca jedynki i zera jest taka sama jak poprzedni układ prawdy/fałszu OR (tabela).
Równanie NOT to:
A = pytanie
Gdzie Q = A i kreska nad A oznacza tutaj uzupełnienie. Uzupełnienie 0 wynosi 1, a uzupełnienie 1 wynosi 0. Bramka NOT jest również nazywana bramką ODWRACAJĄCĄ.
Są to podstawowe (lub pierwiastkowe) tablice prawdy i ich bramki (małe obwody) w elektronice cyfrowej (z algebrą Boole'a). Pozostałe trzy tabele prawdy podane na poniższej ilustracji wraz z ich bramkami służą wyłącznie wygodzie i opierają się na trzech poprzednich tabelach prawdy.
Istnieje tabela prawdy i bramka, które pochodzą z tabeli prawdy i bramki. Nazywa się je tablicą prawdy NAND (od NOT AND) i odpowiadającą jej bramką NAND. Tabela prawdy NAND i jej bramka NAND to:
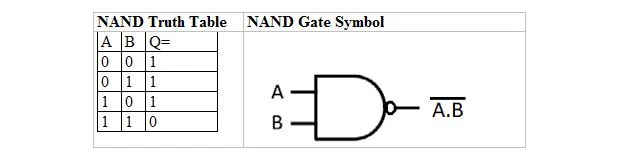
Aby uzyskać tabelę prawdy NAND, przejdź do wyników tabeli prawdy AND i zastąp każdą cyfrę jej uzupełnieniem. Uzupełnienie 0 wynosi 1, a uzupełnienie 1 wynosi 0. Bramka NAND działa jak bramka AND, ale ma małe kółko przed linią wyjściową. Równanie NAND to:
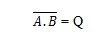
Gdzie oznacza uzupełnienie wyniku „A” I „B”. Pasek (nad linią) jest reprezentowany w bramce przez małe kółko. Należy pamiętać, że kropkę pomiędzy A i B można pominąć.
Istnieje inna tabela prawdy i bramka, które wywodzą się z tabeli prawdy i bramki OR. Nazywa się je tablicą prawdy NOR (od NOT OR) i odpowiadającą jej bramką NOR. Tabela prawdy NOR i jej bramka NOR to:
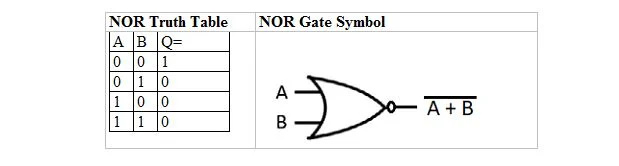
Aby uzyskać tabelę prawdy NOR, przejdź do wyników tabeli prawdy OR i zastąp każdą cyfrę jej uzupełnieniem. Uzupełnienie 0 wynosi 1, a uzupełnienie 1 wynosi 0. Bramka NOR jest podobna do bramki OR, ale ma małe kółko przed linią wyjściową. Równanie NOR to:
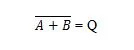
Gdzie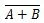 
oznacza uzupełnienie wyniku „A” LUB „B”. Pasek (nadkreślenie) jest reprezentowany w bramce przez małe kółko.
Ekskluzywne LUB (XOR)
Tabela prawdy dla bramki OR to:
W normalnym języku angielskim nie jest jasne, czy ostatni wiersz 1 LUB 1 powinien dać 1 czy 0. Zatem w algebrze Boole'a istnieją dwa rodzaje tablic prawdy OR i dwie odpowiadające im bramki. W przypadku normalnego OR ostatni wiersz 1 OR 1 daje 1. Drugi typ OR to wyłączny OR (XOR), gdzie pierwsze trzy wiersze są takie same, jak pierwsze trzy wiersze normalnego OR (w tym wynik). Jednak w czwartym i ostatnim wierszu 1 LUB 1 daje 0.
Poniższa tabela przedstawia tabelę prawdy XOR i jej symbol bramki XOR (mały obwód):
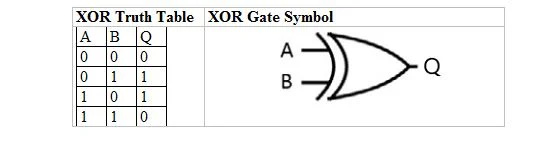
Zarówno w przypadku tablicy prawdy XOR, jak i jej bramki, „A” i „B” są dwiema zmiennymi wejściowymi. „Q” jest zmienną wyjściową.
Równanie XOR to:
A ⊕ B = Q
Gdzie ⊕ oznacza tutaj Boolean XOR.
Normalny OR oznacza jedno lub oba. Ekskluzywne OR oznacza ściśle albo a nie oba.
2.3 Postulaty logiczne
Postulaty to założenia, na podstawie których wyciągane są określone wnioski. Istnieje dziesięć postulatów logicznych, które wywodzą się z równań AND, OR i NOT (tablice prawdy). Równania te nazywane są także funkcjami. Podstawowe funkcje są kopiowane w następujący sposób:
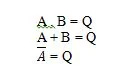
Są to podstawowe funkcje (równania) algebry Boole'a. Poniższe trzy pozostałe równania (funkcje) nie są funkcjami podstawowymi:
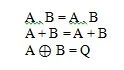
Chociaż ostatnia funkcja jest tutaj osobliwa, nie jest uważana za funkcję podstawową.
Postulaty logiczne są następujące:
Z funkcji AND
1) 0 . 0 = 0
20 . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Z funkcji OR
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Z funkcji NOT
9) 0 = 1
10) 1 = 0
Notatka: Postulaty te to po prostu linie w tabelach prawdy AND, OR i NOT, które są wyrażone w niezależny sposób. Czytelnik powinien zapamiętać podane postulaty.
2.4 Właściwości logiczne
Właściwość to jakby cecha czegoś. Właściwości logiczne to równania wyprowadzone z postulatów Boole'a. W tej sekcji właściwości są po prostu podawane bez wyprowadzeń, a następnie wykorzystywane. Istnieje dwadzieścia pięć właściwości pogrupowanych w dziesięciu nagłówkach w następujący sposób:
Właściwości funkcji AND
Właściwość 1:
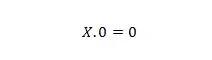
Gdzie X może wynosić 1 lub 0. Oznacza to, że niezależnie od tego, czym jest X, wynikiem jest zawsze 0.
Uwaga: Zmienna nie musi koniecznie oznaczać A, B, C lub D. Zmienna może mieć postać W, X, Y, Z lub dowolnej innej litery.
Właściwość 2:
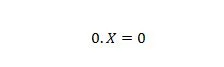
Gdzie X może wynosić 1 lub 0. Należy zauważyć, że różnica między właściwością 1 i właściwością 2 polega na tym, że po lewej stronie znaku równości obu równań pozycje X i 0 są zamienione miejscami.
Właściwość 3:
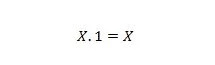
Jeśli X wynosi 0, to 0. 1 = 0. Jeśli X wynosi 1, to 1. 1 = 1.
Właściwość 4:
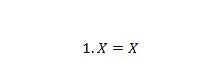
Jeśli X wynosi 0, to 1. 0 = 0. Jeśli X wynosi 1, to 1. 1 = 1. Zauważ, że różnica między właściwością 3 i właściwością 4 polega na tym, że po lewej stronie obu równań pozycje X i 1 są zamienione.
Właściwości funkcji OR
Właściwość 5:
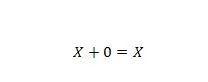
Gdzie X może wynosić 1 lub 0. Oznacza to, że jeśli X wynosi 0, wynikiem jest 0. Jeśli X wynosi 1, wynikiem jest 1.
Właściwość 6:
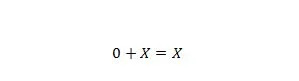
Gdzie X może wynosić 1 lub 0. Należy zauważyć, że różnica między właściwością 5 i właściwością 6 polega na tym, że po lewej stronie obu równań pozycje X i 0 są zamienione miejscami.
Właściwość 7:
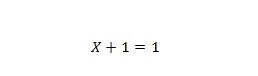
Jeśli X wynosi 0, to 0 + 1 = 1. Jeśli X wynosi 1, to 1 + 1 = 1.
Właściwość 8:
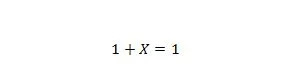
Jeśli X wynosi 0, to 1 + 0 = 1. Jeśli X wynosi 1, to 1 + 1 = 1. Należy zauważyć, że różnica między właściwością 7 i właściwością 8 polega na tym, że po lewej stronie obu równań pozycje X i 1 są zamienione.
Właściwości dotyczące kombinacji zmiennej ze sobą lub z jej uzupełnieniem
Właściwość 9: 
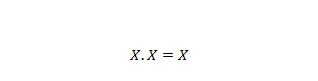
To znaczy: jeśli X wynosi 0, to 0. 0 = 0. Jeśli X wynosi 1, to 1. 1 = 1.
Właściwość 10:
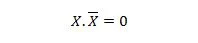
To znaczy: jeśli X wynosi 0, to 0. 1 = 0. Jeśli X wynosi 1, to 1. 0 = 0.
Dla kolejnych zmiennych właściwość ta przyjmuje postać:
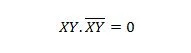
Właściwość 11:
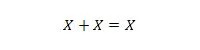
To znaczy: jeśli X wynosi 0, to 0 + 0 = 0. Jeśli X wynosi 1, to 1 + 1 = 1 (z normalnego OR).
Właściwość 12:
To znaczy: jeśli X wynosi 0, to 0 + 1 = 1. Jeśli X = 1, to 1 + 0 = 1.
To znaczy: jeśli X wynosi 0, to 0 + 1 = 1. Jeśli X = 1, to 1 + 0 = 1.
Podwójne uzupełnienie
Właściwość 13:
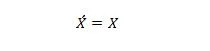
Gdy X po lewej stronie wynosi 0, X po prawej stronie wynosi 0. Gdy X po prawej stronie wynosi 1, X po lewej stronie wynosi 1. Innymi słowy, podwójne uzupełnienie zwraca pierwotną wartość.
Prawo przemienne
Właściwość 14:
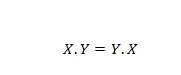
Oznacza to, że zamiana pierwszego i drugiego operandu dla operatora AND po lewej stronie znaku równości nie ma znaczenia; odpowiedź jest nadal taka sama po dokonaniu wymiany po lewej stronie. Równanie to można zapisać pomijając kropki jako: XY = YX.
Właściwość 15:
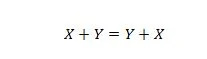
Wyjaśnienie tutaj jest takie samo jak w poprzednim AND, ale dotyczy operatora OR.
Prawo rozdzielcze
Właściwość 16:
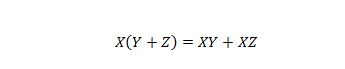
Mamy tu trzy zmienne: X, Y i Z. Każda zmienna może mieć wartość 1 lub 0. Po lewej stronie symbolu równości, nawiasy oznaczają ocenę tego, co się w nich najpierw znajduje. Wtedy AND jest wynikiem X. Prawa strona mówi, że X AND Y razem LUB X AND Z razem są takie same jak lewa strona. Należy zauważyć, że operator kropki dla AND jest w całym tekście pominięty; a połączone zmienne nadal oznaczają AND.
Właściwość 17:
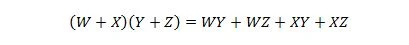
Właściwość ta jest rozszerzeniem właściwości 16 o dodaną zmienną W.
Prawo stowarzyszeniowe
Właściwość 18:
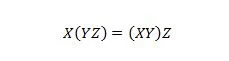
Nawiasy oznaczają najpierw ocenę tego, co jest w nawiasach. Zatem w przypadku wyrażenia po lewej stronie, jeśli Y i Z zostaną najpierw poddane operacji AND, a X zostanie poddane operacji AND z wynikiem, to końcowy wynik po lewej stronie będzie taki sam, jak końcowy wynik po prawej stronie -strona, gdzie X z Y jest najpierw poddawane operacji AND przed wykonaniem operacji AND wyniku z Z. Należy zauważyć, że kropki zostały pominięte w równaniu.
Właściwość 19:
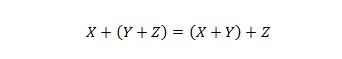
Właściwość tę wyjaśniono w podobny sposób jak właściwość 18, ale zamiast operatora AND zastosowano operator OR. Dla uproszczenia operator OR + nigdy nie jest pomijany w wyrażeniach boolowskich. Z drugiej strony operator AND można pominąć i połączyć obie zmienne.
Wchłanianie
Właściwość 20:
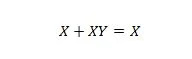
W przypadku tego równania, niezależnie od tego, jakie jest Y, prawa strona zawsze będzie wynosić X (wchłonięta).
Właściwość 21:
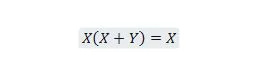
Ponadto w przypadku tego równania, niezależnie od tego, jakie jest Y, prawa strona zawsze będzie wynosić X (wchłonięta). Ta właściwość 21 jest taka sama jak właściwość 20, która jest:
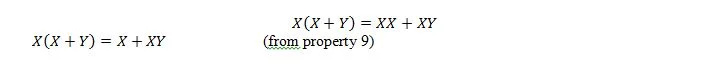
Korzystamy tutaj z prawa rozdzielności i faktu, że X.X = X własności 9.
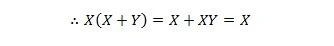
Tożsamość
Właściwość 22:
Oznacza to, że w przypadku wyrażenia X + Y uzupełnienie X przed Y nie zmienia wyrażenia.
Właściwość 23:
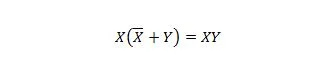
Oznacza to, że w przypadku wyrażenia XY uzupełnienie X OR przez Y w nawiasach, które odbywa się jako pierwsze, nie zmienia wyrażenia XY.
Prawo DeMorgana
Właściwość 24:
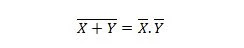
Oznacza to, że bramka NOR (NOT OR) daje taki sam wynik, jak notowanie dwóch wejść przed ich wykonaniem AND.
Właściwość 25:
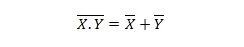
Oznacza to, że bramka NAND (NOT AND) daje taki sam wynik, jak zanotowanie dwóch wejść przed OR.
Dostarczone ilustracje przedstawiają 25 właściwości. Można je udowodnić, podstawiając wszystkie możliwe wartości jedynek i zer w każdym wyrażeniu po lewej stronie, aby sprawdzić, czy otrzymane zostanie wyrażenie (lub wynik) po prawej stronie. Dowody pozostawiamy jako ćwiczenie dla czytelnika.
2.5 Uproszczenie wyrażeń złożonych
Następujące dwie funkcje są takie same:
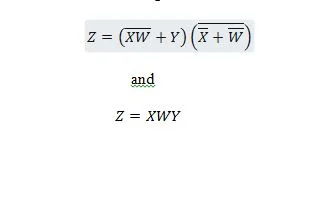
Z to wyjście, a X, W i Y to wejścia. Pierwszy wymaga bramki NAND, bramki OR, bramki AND, dwóch bramek NOT, bramki OR i bramki NOR. Drugi potrzebuje tylko dwóch bramek AND. Pierwsze z nich to równanie z wyrażeniem złożonym po prawej stronie, które zostało uproszczone (zredukowane) do pojedynczego wyrazu prawostronnego dla drugiego równania.
Uproszczenie lub redukcja prowadzi do mniejszej liczby bramek w celu realizacji tej samej funkcji co obwód. Taki mniejszy obwód może być częścią układu scalonego (IC) lub stanowić samodzielny obwód na powierzchni płyty głównej komputera.
Kiedy funkcja (równanie) pojawia się w procesie projektowania, należy dokonać uproszczeń, aby zmniejszyć liczbę bramek i uzyskać tańszy obwód. Uproszczenie wymaga zastosowania jednej lub więcej z poprzednich dwudziestu pięciu właściwości logicznych.
Przykład 2.51:
Skróć równanie:
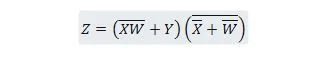
Notatka: Dwa nawiasy obok siebie oznaczają, że nawiasy są połączone operatorem AND (kropka między nimi opcjonalnie nie została wpisana).
Rozwiązanie:
W przypadku rozwiązań uzasadnienie (powód) każdego kroku podane jest po prawej stronie kroku, w nawiasach. Czytelnik powinien zapoznać się z każdym krokiem i jego uzasadnieniem. Czytając kroki redukcji funkcji, czytelnik powinien także odnieść się do poprzednich właściwości.
Przykład 2.52:
Uproszczać:
2.6 Minimalna suma produktów
Następujące dwie funkcje są takie same:
Mówi się, że oba wyrażenia po prawej stronie obu równań mają postać sumy produktów (SP). Mówi się, że wyrażenie ekspresowe ma formę Suma iloczynu, jeśli nie ma nawiasów. Jest oczywiste, że pierwsza funkcja (równanie) potrzebuje więcej bramek niż druga funkcja.
Pierwsze wyrażenie prawostronne można nadal zredukować, aby uzyskać drugą funkcję. Drugiego wyrażenia po prawej stronie nie można już bardziej uprościć i nadal można go wyrazić jako Sumę Produktów („dodanie” terminów). Drugiego wyrażenia po prawej stronie w rzeczywistości nie można już bardziej uprościć. Mówi się zatem, że ma ona formę minimalnej sumy produktów (MSP).
Przykład 2.61:
Najpierw przenieś następującą funkcję do formularza Suma produktów, a następnie do formularza Minimalna suma produktów.
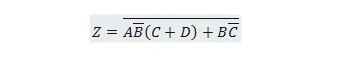
Rozwiązanie:
Rozwiązując takie problemy, należy zastosować jedną lub więcej z poprzednich dwudziestu pięciu właściwości, jak pokazano w tym rozwiązaniu:
2.6 Minimalna suma produktów
Następujące dwie funkcje są takie same:
Mówi się, że oba wyrażenia po prawej stronie obu równań mają postać sumy produktów (SP). Mówi się, że wyrażenie ekspresowe ma formę Suma iloczynu, jeśli nie ma nawiasów. Jest oczywiste, że pierwsza funkcja (równanie) potrzebuje więcej bramek niż druga funkcja.
Pierwsze wyrażenie prawostronne można nadal zredukować, aby uzyskać drugą funkcję. Drugiego wyrażenia po prawej stronie nie można już dalej upraszczać i nadal można go wyrazić jako Sumę Produktów („dodanie” terminów). Drugiego wyrażenia po prawej stronie w rzeczywistości nie można już bardziej uprościć. Mówi się zatem, że ma ona formę minimalnej sumy produktów (MSP).
Przykład 2.61:
Najpierw przenieś następującą funkcję do formularza Suma produktów, a następnie do formularza Minimalna suma produktów.
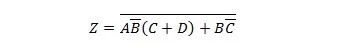
Rozwiązanie:
Rozwiązując takie problemy, należy zastosować jedną lub więcej z poprzednich dwudziestu pięciu właściwości, jak pokazano w tym rozwiązaniu:
To ostatnie wyrażenie jest w formie sumy produktów (SP), ale nie w formie minimalnej sumy produktów (MSP). Odpowiedź na pierwszą część pytania została udzielona. Rozwiązanie drugiej części jest następujące:
Ta ostatnia uproszczona funkcja (równanie) ma postać MSP i wymaga do realizacji mniejszej liczby bramek niż odpowiadająca jej postać SP. Pamiętaj: SP oznacza Sumę Produktów, natomiast MSP oznacza Minimalną Sumę Produktów.
Przykład 2.62:
Poniższy obwód ma wejścia X, Y i W, a Z jest wyjściem. Utwórz funkcję sumy produktów (SP) (funkcja pozornej minimalnej sumy produktów) dla Z. Następnie utwórz prawdziwą, bardziej zmniejszoną (zminimalizowaną) sumę produktów (MSP). Następnie zaimplementuj obwód MSP (narysuj sieć bramkową MSP).
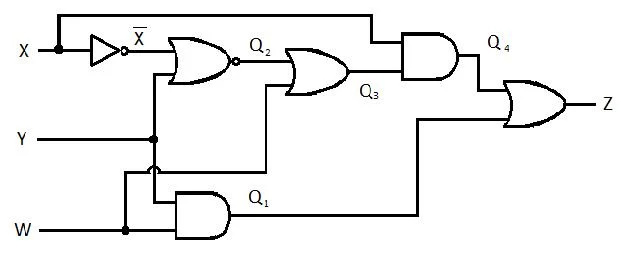
Rys. 2.61 Obwód bramkujący
Rozwiązanie:
Przed rozpoczęciem procesu upraszczania wyrażenie Z należy uzyskać w postaci X, Y i W. Zapoznaj się z tą przykładową ilustracją ze diagramu:
Jest to wyrażenie Z w kategoriach X, Y i W. Następnie można dokonać uproszczenia do pozornego MSP. Pozornym MSP jest SP.
To ostatnie równanie (funkcja) ma postać SP. To nie jest prawda Minimalna Suma Produktów (jeszcze nie MSP). Zatem redukcja (minimalizacja) musi być kontynuowana.
To ostatnie równanie (funkcja) jest prawdziwą minimalną sumą produktów (MSP). Minimalna suma produktów (prawdziwa minimalizacja) obwodu bramkowego wynosi:
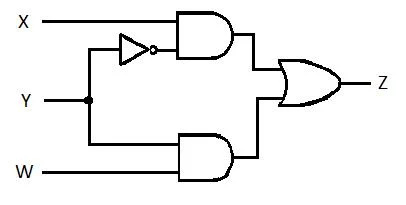
Rys. 2.62 Obwód bramkujący MSP
Komentarz
Z analizy przeprowadzonej w tej sekcji widać, że nie jest jasne, czy Suma Produktów jest Minimalną Sumą Produktów, czy nie. SP nie jest zbyt przydatny. Bardzo przydatne jest MSP. Istnieje pewny sposób na uzyskanie MSP; polega na użyciu mapy Karnaugh. Mapa Karnaugh wykracza poza zakres tego internetowego kursu kariery.
2.7 Problemy
Czytelnikowi zaleca się rozwiązanie wszystkich problemów zawartych w danym rozdziale przed przejściem do następnego rozdziału.
- Utwórz tablice prawdy AND, OR i NOT wraz z odpowiadającymi im bramkami.
- Zapisz dziesięć postulatów logicznych w ich różnych kategoriach, nadając im nazwy.
- Bez wyjaśnień zapisz dwadzieścia sześć właściwości algebry Boole'a w ich różnych kategoriach, nadając im nazwy.
- Zredukuj równanie, korzystając z właściwości logicznych i podając użyte kategorie.
- Zredukuj równanie, korzystając z właściwości logicznych i podając użyte kategorie.
- Korzystając z właściwości Boolean i podając użyte kategorie, sprowadź poniższe równanie – najpierw do Sumy Produktów, a następnie do Minimalnej Sumy Produktów:
- Korzystając z właściwości Boolean i podając użyte kategorie, sprowadź poniższe równanie – najpierw do Sumy Produktów, a następnie do Minimalnej Sumy Produktów:
